home">bauhome -  gefördert vom bm:bwk im Rahmen des Projektes "Neue Medien im Unterricht an Universitäten und Fachhochschulen"
Normale Axonometrie
 

Normalaxonometrische Risse wirken anschaulicher als Schrägrisse.
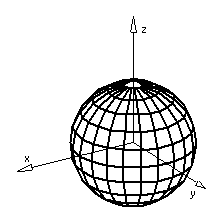
Das normalaxonometrische Bild einer Kugel ist ein Kreis. Dieser entsteht als Schnitt des Sehzylinders um die Kugel mit der Bildebene . Da dieser Sehzylinder normal auf die Bildebene steht, ist die Schnittkurve ein Normalschnitt des Kreiszylinders und somit ein Kreis.

Im Gegensatz dazu ist ein Schrägriss einer Kugel eine Ellipse, die als Schnitt eines nicht auf orthogonal stehenden Sehzylinders mit der Bildebene entsteht.

Bei der normalen Axonometrie ist die Projektionsrichtung p normal zur Bildebene . Keine Koordinatenebene darf projizierende Lage haben und keine Koordinatenachse darf Hauptlage haben.

Schneidet man die x-, y- und z-Achse mit der Bildebene , so sind die Schnittpunkte X, Y und Z die Spurpunkte der Achsen in der Bildebene . Die Normalrisse der Achsen enthalten diese Spurpunkte. Die Verbindung ist eine Hauptgerade der xy-Ebene (da sie in der Bildebene liegt). Da die Grundrissebene mit der z-Achse einen rechten Winkel einschließt und h  Hauptgerade der Grundrissebene ist, ist der rechte Winkel zwischen und ersichtlich. Es gilt also . Analog sind und Hauptgeraden der yz-Ebene bzw. zx-Ebene und es gilt und .
Das Dreieck ist also ein Hauptgeradendreieck. Die Höhenlinien, also die Normalen auf , und durch Z, X und Y.  von sind die normalaxonometrischen Risse der Achsen. Der Höhenschnittpunkt von ist Bild des Koordinatenursprungs U.
liegt innerhalb des Dreiecks , da  und weiters  gilt (analog für die beiden anderen Dreieckshöhen).  Das Dreieck ist somit spitzwinkelig, denn nur bei spitzwinkeligen Dreiecken liegt der Höhenschnittpunkt im Inneren des Dreiecks.


 

Drei Geraden durch einen gemeinsamen Punkt, von denen jede im stumpfen Winkel der beiden anderen liegt, können stets als Normalrisse von drei paarweise orthogonalen Geraden aufgefasst werden.

Die Verzerrungen der drei Achsen sind durch deren normalaxonometrische Angaben schon mitbestimmt. Man dreht die xy-Ebene um die Hauptgerade in die Bildebene. Dabei wandert jeder Punkt auf einem Drehkreis. Die Drehkreisebenen sind normal zur Hauptgeraden und erscheinen daher im normalaxonometrischen Riss projizierend. Das normalaxonometrische Bild der Drehkreisebene durch U fällt daher mit zusammen, und der Normalriss der gedrehten Lage liegt auf dem Bild der z-Achse. Der Normalriss der gedrehten Achsen zeigt den eingeschlossenen rechten Winkel unverzerrt.  Die  Punkte X, Y bleiben bei der Paralleldrehung von fest, liegt daher auf dem Halbkreis (Thaleskreis) mit dem Durchmesser .
Die Verzerrungen ,  der x- bzw. y-parallelen Strecken sind mitbestimmt. Dreht man auch noch die Ebene um ihre Hauptgerade in die Bildebene erhält man  die Verzerrung der z-parallelen Strecken .

Isometrie: Die Isometrie ist eine spezielle normalaxonometrische Angabe. Hier gilt . Also sind die einschließenden Achsenwinkel alle 120° groß. Die Verzerrungen der drei Koordinatenachsen sind gleich: .

                     

Konstruieren Sie nun mit Zirkel und Lineal ein normalaxonometrisches Bild einer Pyramide. Drucken  Sie das Angabeblatt aus oder wählen Sie eine Angabe Ihrer Wahl nach den eben besprochenen Kriterien. Film
Mit bestem Dank an Herrn Georg Schindl (Studierender der FH-Bau) für die Umsetzung meiner Bilder zu einer Animation.